Большая Советская
Энциклопедия
|
|
|
|
источник статьи: Большая Советская Энциклопедия |
|
Параболоиды (от парабола и греч. éidos — вид), незамкнутые поверхности второго порядка, не имеющие центра. Различают два вида П.: эллиптический П. (рис. 1) и гиперболический П. (рис. 2). П. представляют собой два типа из общего числа пяти основных типов поверхностей второго порядка. Линиями пересечения гиперболического П. со всевозможными плоскостями пространства являются гиперболы, параболы и прямые. Через каждую точку гиперболического П. проходят две прямолинейные образующие, и, таким образом, гиперболический П. представляет собой линейчатую поверхность. Для эллиптического П. существуют плоскости, не пересекающиеся с ним. Если же плоскость пересекается с эллиптическим П., то линией пересечения является либо эллипс, либо парабола. В надлежащей системе координат уравнения П. имеют вид: x2/2p + y2/2q = z (эллиптический П.), x2/2p — y2/2q = z (гиперболический П.); здесь р > 0 и q > 0. 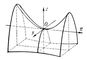 Рис. 2. Гиперболический параболоид. 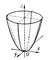 Рис.1. Эллиптический параболоид. |