Большая Советская
Энциклопедия
|
|
|
|
источник статьи: Большая Советская Энциклопедия |
|
Гиперболические функции, функции, определяемые формулами: (гиперболический синус), (гиперболический косинус). Иногда рассматривается также гиперболический тангенс: (графики Г. ф. см. на рис. 1). Г. ф. связаны между собой соотношениями, аналогичными соотношениям между тригонометрическими функциями: Г. ф. можно выразить через тригонометрические: Геометрически Г. ф. получаются из рассмотрения равнобочной гиперболы х2—у2 = 1, которую можно задать параметрическими уравнениями х = ch t, у = sh t, аргумент t представляет двойную площадь сектора гиперболы ОАС (см. рис. 2). Обратные Г. ф. (ареа-синус гиперболический и ареа-косинус гиперболический) определяются формулами:
Лит.: Янпольский A. Р., Гиперболические функции, М., 1960. 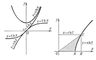 Рис. 1 — слева, и рис. 2 — справа к ст. Гиперболические функции. |